Universal framework with exponential speedup for the quantum simulation of quantum field theories including QCD

Abstract

We present a quantum simulation framework universally applicable to a wide class of quantum systems, including quantum field theories such as quantum chromodynamics (QCD). Specifically, we generalize an efficient quantum simulation protocol developed for bosonic theories in [Halimeh et al., arXiv:2411.13161] which, when applied to Yang-Mills theory, demonstrated an exponential resource advantage with respect to the truncation level of the bosonic modes, to systems with both bosons and fermions using the Jordan-Wigner transform and also the Verstraete-Cirac transform. We apply this framework to QCD using the orbifold lattice formulation and achieve an exponential speedup compared to previous proposals. As a by-product, exponential speedup is achieved in the quantum simulation of the Kogut-Susskind Hamiltonian, the latter being a special limit of the orbifold lattice Hamiltonian. In the case of Hamiltonian time evolution of a theory on an  spatial lattice via Trotterization, one Trotter step can be realized using  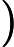numbers of CNOT gates, Hadamard gates, phase gates, and one-qubit rotations. We show this analytically for any matter content and  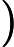gauge group with any . Even when we use the Jordan-Wigner transform, we can utilize the cancellation of quantum gates to significantly simplify the quantum circuit. We also discuss a block encoding of the Hamiltonian as a linear combination of unitaries using the Verstraete-Cirac transform. Our protocols do not assume oracles, but rather present explicit constructions with rigorous resource estimations without a hidden cost, and are thus readily implementable on a quantum computer.